State machine

Table of Contents

The blockchain state as Sparse Merkle Tree
Use cases of Merkle trees in Klayr

Every blockchain is at its core a replicated deterministic finite-state machine.

A state machine is a concept in computer science, consisting of the following elements:
- States: A state machine typically has a set of different states that it can enter. For example, a padlock represented as a state machine would have the two states "Open" and "Locked".
- Transitions: A set of allowable operations that change from one state to another. For example, to change from the state "Open" to "Locked", a transition would be "Close padlock", and from "Locked" to "Open", it would be "Insert key & turn".
The state machine is replicated across multiple nodes. Each node maintains independently the current state of the state machine. This only works for deterministic state machines.
Finite means that the number of states that the machine can reach is finite (not infinite).
And deterministic means that if the state machine is replicated and all state transitions are replayed, it will end up always in the exact same state.

In the blockchain context, these elements are represented as follows:

A state is a state of the blockchain. In Klayr, a key-value store is used as a database, containing all data that is considered part of the blockchain.
A transition of states is triggered through blocks and their containing transactions which are added to the blockchain. When executing a block B, the state machine changes its state from a state S to a state S’. This one state transition can further be broken down into smaller intermediate state transitions, for instance, by considering that executing a block means executing all transactions in that block sequentially.

The blockchain state as Sparse Merkle Tree

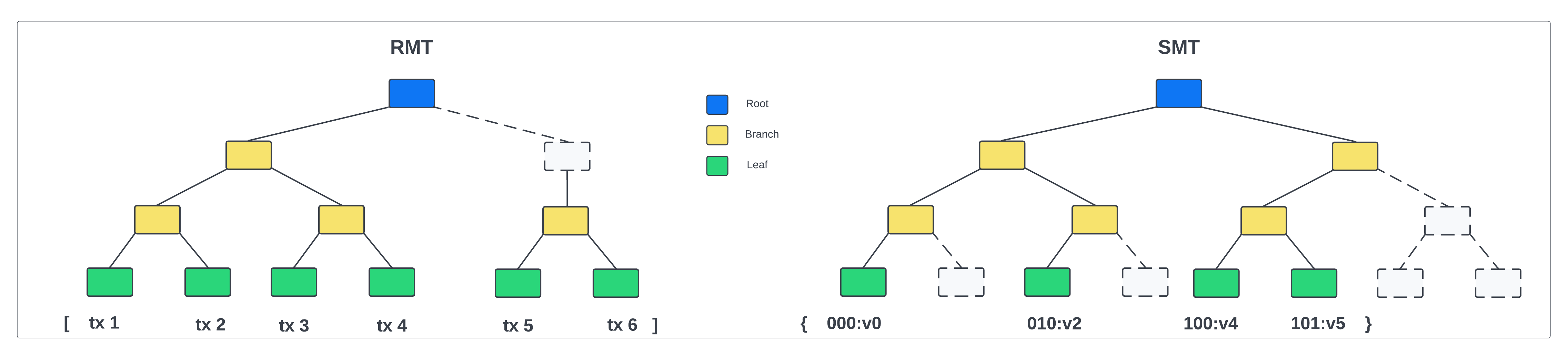
A Regular Merkle Tree (RMT) is an authenticated data structure organized as a tree. Let’s try to understand what exactly each of these words means:

Merkle: This name is derived from the actual inventor of hash trees, Ralph Merkle.
Data structure: A data structure is a collection of data with a set of operations that can be performed on it. An example of a data structure is an array, an object, or a Merkle tree.
Authenticated: The integrity of the data structure can be efficiently verified using the (Merkle) root of the tree. The dataset cannot be altered without changing the Merkle root.
Tree: The underlying data structure is organized as a tree, where each parent node is obtained by hashing the data from the child nodes in the layer below. Here we consider only binary trees, where each parent has two children.

A Sparse Merkle Tree (SMT) is very similar to a Regular Merkle Tree, with the following difference: The order of insertion of data blocks does not matter, and the root of the tree only depends on the final state of the map. That means, in an SMT, the input of the hash function is the underlying key-value map and the output is the Merkle root.

Due to the history independence, SMTs are the suitable choice to authenticate key-value maps.

Figure 1. RMT vs SMT

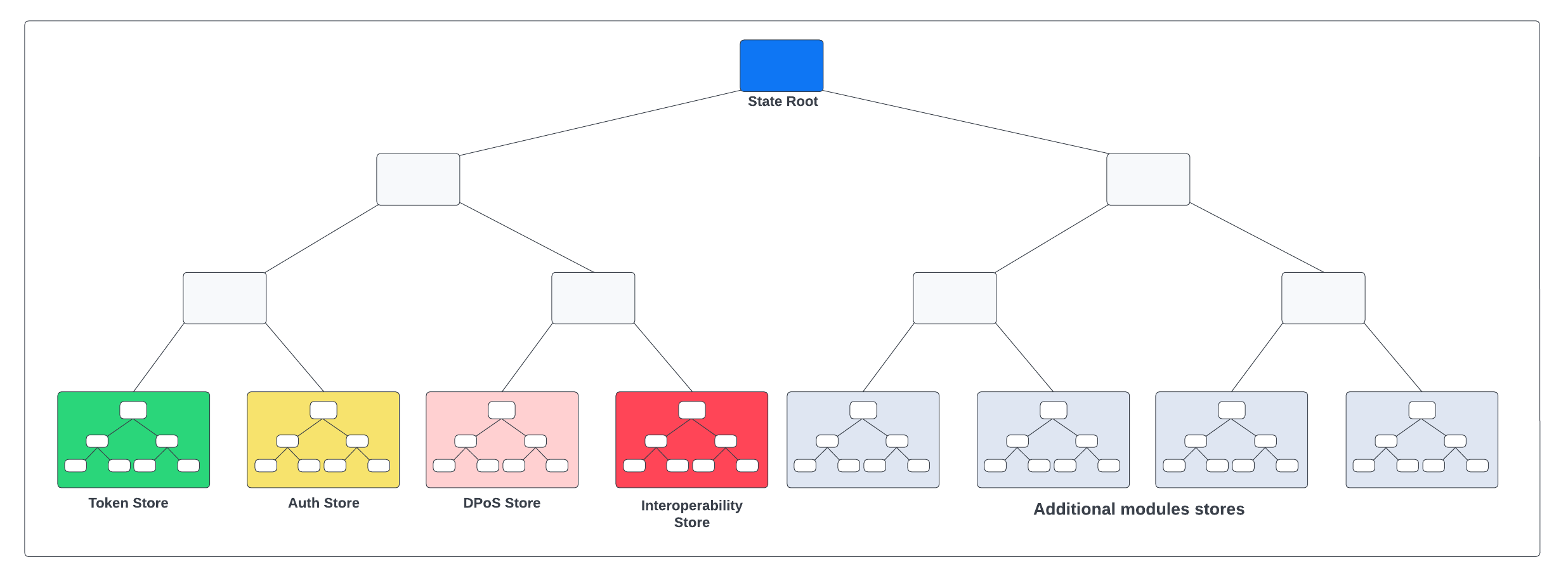
A blockchain created with the Klayr SDK defines a single global store. An SMT is created on top of the global state store, called the state tree. Then the Merkle root of this tree, the state root, is inserted into each block header.

Each module registered on the chain defines its own generic key-value map, where:

key: Store Prefix + Substore prefix + sha256(Store key)
- Store prefix: The module store prefix is calculated automatically from the first 4 bytes of the hash of the module name, where the first bit of the store prefix is set to 0. The module name is the unique identifier of the module, identifying the key-value map. On the other hand, the Interoperability module store prefix is set to a constant, with the first bit set to 1. This is done to separate the Interoperability module from other modules in the state tree and make the state tree unbalanced, to shorten inclusion proofs for the Interoperability module store (required for cross-chain update commands).
- Substore prefix The substore prefix identifies a substore within the module store, i.e., a group of key-value pairs with the same scope and typically values in the same format. Substore prefixes are byte values, having a length of 2 bytes.
- sha256(Store key): Here we take the hash of the store key which identifies a certain element within a store bucket.
Store value: serialized object (with JSON schema)
- JSON schema: The schema used in klayr-codec to serialize the value

Figure 2. Module data stores of a sidechain as SMT

Use cases of Merkle trees in Klayr

SMTs allow efficient inclusion & non-inclusion proofs

A Prover is able to convince a Verifier that a certain element is present in the underlying data structure without revealing any other element, and the proof size scales logarithmically with the number of data blocks. A Prover can convince a Verifier that a certain entry is not present in the map, and the proof size scales logarithmically with the number of data blocks.

A list of all use cases for SMTs in the Klayr Protocol, and their corresponding SMT is described below:

Table 1. Use cases for SMTs in the Klayr protocol
Use Case	SMT	Description
Interoperability	`stateRoot`	The `stateRoot` is used during the processing of cross-chain update transactions to authenticate the outgoing messages from one chain.
State consistency	`stateRoot`	All nodes in the network will be able to check the consistency of the state just by checking the `stateRoot`. For instance, if a block contains a transaction that randomly credits either user A or user B with tokens, then any node obtaining a different result from the block generator would immediately reject the block, as the two state roots would differ.
Light clients	`stateRoot`	The `stateRoot` can be used to provide efficient proofs for the state of a certain account.
Decentralized Regenesis	`stateRoot`	A snapshot of the blockchain can be used to perform a hardfork to implement the new protocol. Reference to the last blockchain state will be stored as the Merkle root of the hashes of all blocks up to the snapshot.
Proofs-of-Inclusion for Events in a Block	`eventRoot`	The root of the event Sparse Merkle Tree is added to the block header to allow checking the inclusion and non-inclusion of events.

A list of all use cases for RMTs in the Klayr Protocol, and their corresponding RMT is described below:

Table 2. Use cases for RMTs in the Klayr protocol
Use Case	RMT	Description
Proofs-of-Inclusion for Transactions in a Block	`transactionRoot`	Each block header stores the `transactionRoot`. The `transactionRoot` is calculated as the Merkle root of the IDs of the transactions included in the block payload^[1]. Using the `transactionRoot` and a proof-of-inclusion, it is possible to check whether a certain transaction is part of the block without downloading the full block. 1. The details are specified in LIP 0032.
Proofs-of-Inclusion for Assets in a Block	`assetRoot`	The root of the asset Merkle tree is added to the block header to allow checking the inclusion and non-inclusion of block assets.
Inbox & Outbox	`inboxRoot`, `outboxRoot`	Since the root of the tree depends on the order of insertion, all cross-chain messages have to be inserted in the receiving chain in the same order in which they were included in the sending chain, guaranteeing that they are processed in the correct order. Using a Merkle tree also guarantees that the number of sibling hashes that are part of inclusion proofs grows only logarithmically with the number of elements in the tree. In particular, this means that the number of sibling hashes required to validate the cross-chain messages in a CCU against the partner chain `lastCertificate.stateRoot` grows logarithmically with the number of processed messages.

What are key-value maps?

A key-value map is a collection of (key, value) pairs such that each key appears at most once. It supports the following operations:

Look up: Returns the value associated with a certain key.
Insert: Inserts a certain key-value pair in the collection.
Update: Updates the value associated with a certain key.
Delete: Removes a certain key-value pair in the collection.

For more information about RMTs and SMTs, check out the following blog posts: